Dezembro de 2016 na praça Ricardo Lessa no Dubeux Leão,em comemoração ao dia da Bíblia Sagrada.
sexta-feira, 24 de fevereiro de 2017
quinta-feira, 23 de fevereiro de 2017
quarta-feira, 22 de fevereiro de 2017
THERE IS E THERE ARE
There is e there are (verbo there to be)
Este post já foi lido 5210 vezes desde 27/06/2015
AddThis Sharing Buttons
O post de hoje foi sugestão de uma leitora, que perguntou no Facebook a diferença entre there is e there are. Já fiz um post falando sobre isso,
porém hoje vou tentar reescrever de uma maneira mais didática. Em todo
caso, faça uma visita ao outro post para ver vários exemplos de uso.
Os verbos there is e there are são conjugações do verbo there to be. Ele é usado quando queremos dizer que existe (ou não) algo, alguém ou alguma situação no momento. Pode ser traduzido como haver ou existir.
Importante: em português costumamos usar o verbo ter também neste contexto, e é comum ao iniciarmos o estudo do inglês dizermos coisas do tipo “Has one plate on the table” para dizer que “Tem (existe, há) um prato sobre a mesa”. Não se usa o verbo to have neste sentido.
COMO USAR O VERBO THERE TO BE?
Ao contrário da maioria absoluta dos
verbos em inglês, este verbo não se liga a nenhum sujeito (ele está
sempre solteiro..risos). O que determina se devemos usar there is ou there are é se o que está sendo mencionado na frase está no singular ou no plural.
Para o singular se usa there is e para o plural se usa there are. Simples assim.
Você não irá usar frases como he there is ou we there are. Isso non ecziste. 

Veja alguns exemplos:
- There are two hundred thousand people in my city. (Há 200 mil pessoas em minha cidade)
- There is a fly in your soup. (Há uma mosca na sua sopa)
Os exemplos acima estão na forma afirmativa, no presente. Falarei sobre o passado e o futuro em outro post.
Para fazer a forma negativa, é só acrescentar not após o is/are: There is not/There are not. As duas frases acima ficariam There are not two hundred thousand people in my city e There is not a fly in your soup.
A forma interrogativa inverte põe o is/are na frente do there. E, logicamente, tem um ponto de interrogação no final da frase. 

- Are there two hundred people in your city? (Há 200 mil pessoas na sua cidade?)
- Is there a fly in your soup? (Há uma mosca na sua sopa?)
DÁ PRA CONTRAIR?
Sim, dá.
Na forma afirmativa, there is fica there’s (There’s a fly…). Com relação ao b, existe a contração there’re, mas é muito raro se ver e muita gente considera estranho (eu inclusive). Prefira o there are mesmo.
Na forma negativa, você pode contrair o there is not de duas formas: there’s not ou there isn’t. Já o there are not fica there aren’t.
A forma interrogativa não tem contração.
POTENCIAÇÃO
A potenciação ou exponenciação é a operação de elevar
um número ou expressão a uma dada potência. Para entendermos o
significado disto, observe a figura em vermelho à direita:
Note que temos o número dois ( 2 ) com o número três ( 3 ) sobrescrito à sua direita ( 23 ). Dizemos que o número 2 está elevado à terceira potência, ou ainda que 23 é a terceira potência de 2.
Nesta potência o número 2 é a sua base e ao número 3 damos o nome de expoente.
Esta potência representa a multiplicação de três fatores iguais a dois, então 23 é igual a 2 . 2 . 2 que é igual a 8.
Potências com expoente 2 ou 3 possuem uma outra forma particular de leitura. A potência 23 também pode ser lida como dois ao cubo, assim como a potência 32 pode ser lida como três ao quadrado.
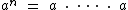 , isto é, a multiplicação de n fatores iguais a a.
, isto é, a multiplicação de n fatores iguais a a.
Este é o caso de mais fácil compreensão, pois o conceito da exponenciação está bem claro. Observe a expressão abaixo:

54, que se lê 5 elevado a 4, ou 5 elevado à quarta potência é igual ao produto de quatro fatores todos eles iguais a cinco. Ao multiplicarmos 5 vezes 5 vezes 5 vezes 5 iremos obter 625 que é o resultado da exponenciação. O número de fatores iguais a 5 é justamente o numeral do expoente.
Apesar de estarmos trabalhando com expoentes inteiros, as bases podem ser decimais:

Assim como também podem ser fracionárias:
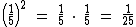


00 é indeterminado, embora em algumas situações convenciona-se que seja igual a 1. Para qualquer outro expoente real n positivo, temos que 0n = 0.
Mais à frente teremos outras informações que nos levarão a concluir que 00 = 0/0 e como não existe divisão por zero no conjunto dos números reais, trata-se então de uma indeterminação.
Ao estudarmos os expoentes negativos, a seguir, poderemos concluir que 0n é indefinido para qualquer n real negativo, por exemplo, 0-2 pode ser expresso como 1/02, o que nos leva à 1/0 e como sabemos, a divisão real de 1 por 0 é indefinida, pois não existe nenhum número real que multiplicado por 0 resulte em 1.
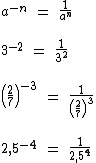
Vejamos agora a explicação onde se baseiam estes três últimos conceitos explicados acima.

Primeiramente vamos substituir as potências por suas respectivas multiplicações:

Repare que a expressão foi substituída pela multiplicação de 7 fatores iguais a a.
Pelo conceito da exponenciação podemos então escrever a seguinte potência:

De onde concluímos que:

Generalizando:

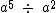
Substituindo as potências por suas respectivas multiplicações:

Utilizamos uma fração ao invés do operador ,
apenas para visualisarmos mais facilmente o próximo passo, que será a
simplificação de dois fatores do numerador com dois fatores do
denominador:
,
apenas para visualisarmos mais facilmente o próximo passo, que será a
simplificação de dois fatores do numerador com dois fatores do
denominador:

Do estudado até agora sabemos que:

Então chegamos a conclusão de que:
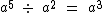
Novamente generalizando temos:

Note que a base a deve ser diferente de 0, pois como sabemos não existe quociente real para a divisão por zero neste conjunto numérico.

Então se tivermos m = n temos que:

Sabemos que:
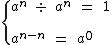
Já todo número, diferente de zero, dividido por ele mesmo é igual a 1 e que todo número menos ele mesmo é igual a zero.
Logo concluímos que:
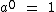
É por isto que todo número, diferente de zero, elevado a 0 é igual a 1:

Logo se tivermos m = n + 1 temos que:

Como:

Então:
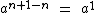
Logo:

Agora vamos transformar as potências do primeiro membro em multiplicações do fator a:
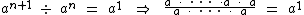
Repare que o numerador da fração no primeiro membro possui um fator a a mais que o denominador, pois o expoente da potência do numerador tem uma unidade a mais que o expoente da potência do denominador. Simplificando a fração temos:

Ou ainda:

Uma outra forma de entendermos porque a1 = a é que pela própria definição de potência, o expoente indica o número de fatores e como o expoente é igual a 1, obviamente este fator será o próprio número.

Se tivermos m = 0:

Como a0 = 1, temos:

Ou:
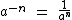

Vamos tomar como exemplo o produto de três fatores distintos elevados ao cubo:
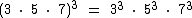
Não custa nada fazermos uma verificação só para conferir:


Exemplo:

Vamos verificar:


Exemplo:
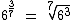
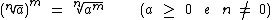
Exemplo:


Vamos como de costume recorrer a um exemplo:

E agora vamos verificar a veracidade desta propriedade:


Qual é a razão desta desigualdade?
No caso de devemos calcular
devemos calcular 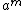 primeiro por causa da precedência dos parênteses, o que está entre parênteses deve ser calculado primeiro. Já no caso de
primeiro por causa da precedência dos parênteses, o que está entre parênteses deve ser calculado primeiro. Já no caso de  devemos calcular
devemos calcular 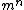 primeiro, pois neste caso a precedência é calcularmos do expoente mais externo para o mais interno.
primeiro, pois neste caso a precedência é calcularmos do expoente mais externo para o mais interno.
Usemos como exemplo a expressão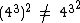 para verificarmos a desigualdade:
para verificarmos a desigualdade:
No primeiro membro iremos resolver primeiro 43 que é igual a 64, já no segundo membro vamos resolver primeiro 32 que é igual a 9:
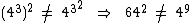
Finalmente vamos elevar 64 ao quadrado e 4 à nona potência:

Alternativamente também podemos realizar as seguintes operações, multiplicando os expoentes da potência do primeiro membro:


Note que temos o número dois ( 2 ) com o número três ( 3 ) sobrescrito à sua direita ( 23 ). Dizemos que o número 2 está elevado à terceira potência, ou ainda que 23 é a terceira potência de 2.
Nesta potência o número 2 é a sua base e ao número 3 damos o nome de expoente.
Esta potência representa a multiplicação de três fatores iguais a dois, então 23 é igual a 2 . 2 . 2 que é igual a 8.
Potências com expoente 2 ou 3 possuem uma outra forma particular de leitura. A potência 23 também pode ser lida como dois ao cubo, assim como a potência 32 pode ser lida como três ao quadrado.
Potências de Base Real com Expoente Inteiro
Nestas condições há quatro situações em particular que
iremos tratar. A saber, quando o expoente é maior que um, quando é igual
a um, quando é igual a zero e quando é negativo.
Expoente Maior que 1
De forma geral:
Este é o caso de mais fácil compreensão, pois o conceito da exponenciação está bem claro. Observe a expressão abaixo:
54, que se lê 5 elevado a 4, ou 5 elevado à quarta potência é igual ao produto de quatro fatores todos eles iguais a cinco. Ao multiplicarmos 5 vezes 5 vezes 5 vezes 5 iremos obter 625 que é o resultado da exponenciação. O número de fatores iguais a 5 é justamente o numeral do expoente.
Apesar de estarmos trabalhando com expoentes inteiros, as bases podem ser decimais:
Assim como também podem ser fracionárias:
Expoente Igual a 1
Todo número elevado a 1 é igual ao próprio número:
Expoente Igual a 0
Todo número, diferente de zero, elevado a 0 é igual a 1:
00 é indeterminado, embora em algumas situações convenciona-se que seja igual a 1. Para qualquer outro expoente real n positivo, temos que 0n = 0.
Mais à frente teremos outras informações que nos levarão a concluir que 00 = 0/0 e como não existe divisão por zero no conjunto dos números reais, trata-se então de uma indeterminação.
Ao estudarmos os expoentes negativos, a seguir, poderemos concluir que 0n é indefinido para qualquer n real negativo, por exemplo, 0-2 pode ser expresso como 1/02, o que nos leva à 1/0 e como sabemos, a divisão real de 1 por 0 é indefinida, pois não existe nenhum número real que multiplicado por 0 resulte em 1.
Expoente Negativo
Qualquer número diferente de zero elevado a um expoente negativo é igual ao inverso deste número elevado ao oposto do expoente:
Vejamos agora a explicação onde se baseiam estes três últimos conceitos explicados acima.
Propriedades das Potências de Base Real com Expoente Inteiro
Multiplicação de Potências de Mesma Base
A multiplicação de potências de mesma base é igual a esta base elevada à soma dos expoentes.
Vamos analisar o desenvolvimento da expressão a elevado à quinta potência vezes a elevado ao quadrado para confirmarmos esta afirmação:Primeiramente vamos substituir as potências por suas respectivas multiplicações:
Repare que a expressão foi substituída pela multiplicação de 7 fatores iguais a a.
Pelo conceito da exponenciação podemos então escrever a seguinte potência:
De onde concluímos que:
Generalizando:
Divisão de Potências de Mesma Base
A divisão de potências de mesma base, diferente de zero, é igual a esta base elevada à diferença dos expoentes.
Vamos utilizar as mesmas potências analisadas na propriedade anterior, mas agora fazendo a análise em relação à divisão:Substituindo as potências por suas respectivas multiplicações:
Utilizamos uma fração ao invés do operador
Do estudado até agora sabemos que:
Então chegamos a conclusão de que:
Novamente generalizando temos:
Note que a base a deve ser diferente de 0, pois como sabemos não existe quociente real para a divisão por zero neste conjunto numérico.
Entendendo porque a0 = 1
Para a ≠ 0 sabemos que:Então se tivermos m = n temos que:
Sabemos que:
Já todo número, diferente de zero, dividido por ele mesmo é igual a 1 e que todo número menos ele mesmo é igual a zero.
Logo concluímos que:
É por isto que todo número, diferente de zero, elevado a 0 é igual a 1:
Entendendo porque a1 = a
Para a ≠ 0 sabemos que:Logo se tivermos m = n + 1 temos que:
Como:
Então:
Logo:
Agora vamos transformar as potências do primeiro membro em multiplicações do fator a:
Repare que o numerador da fração no primeiro membro possui um fator a a mais que o denominador, pois o expoente da potência do numerador tem uma unidade a mais que o expoente da potência do denominador. Simplificando a fração temos:
Ou ainda:
Uma outra forma de entendermos porque a1 = a é que pela própria definição de potência, o expoente indica o número de fatores e como o expoente é igual a 1, obviamente este fator será o próprio número.
Entendendo porque a-n = 1/an
Como já vimos para a ≠ 0 temos que:Se tivermos m = 0:
Como a0 = 1, temos:
Ou:
Potência de um Produto
A potência do produto de dois ou mais fatores é igual ao produto de cada um destes fatores elevados ao expoente em questão:
Vamos tomar como exemplo o produto de três fatores distintos elevados ao cubo:
Não custa nada fazermos uma verificação só para conferir:
Potência de um Quociente
Podemos proceder de forma análoga ao que fizemos no caso
da multiplicação, mas neste caso os divisores não podem ser iguais a
zero:
Exemplo:
Vamos verificar:
Potência de um Expoente Fracionário
Podemos transformar uma potência com expoente fracionário em um radical:
Exemplo:
Potência de uma Raiz
Ao elevarmos um radical
a uma dada potência, estaremos obtendo o mesmo resultado que obteríamos
se elevássemos apenas o seu radicando a esta mesma potência:
Exemplo:
Potência de uma Potência
Novamente para uma base diferente de zero podemos expressar a seguinte igualdade:
Vamos como de costume recorrer a um exemplo:
E agora vamos verificar a veracidade desta propriedade:
Você sabe por que 2 + 3 . 5 é igual a 17 e não igual a 25?
Simplesmente porque o operador da multiplicação tem precedência sobre o operador da adição. Você deve primeiro realizar a multiplicação e depois a adição. Agora veja a expressão abaixo:Qual é a razão desta desigualdade?
No caso de
Usemos como exemplo a expressão
No primeiro membro iremos resolver primeiro 43 que é igual a 64, já no segundo membro vamos resolver primeiro 32 que é igual a 9:
Finalmente vamos elevar 64 ao quadrado e 4 à nona potência:
Alternativamente também podemos realizar as seguintes operações, multiplicando os expoentes da potência do primeiro membro:
Assinar:
Comentários (Atom)
