Mostrando postagens com marcador POTENCIAÇÃO. Mostrar todas as postagens
Mostrando postagens com marcador POTENCIAÇÃO. Mostrar todas as postagens
sexta-feira, 21 de abril de 2017
quarta-feira, 22 de fevereiro de 2017
POTENCIAÇÃO
A potenciação ou exponenciação é a operação de elevar
um número ou expressão a uma dada potência. Para entendermos o
significado disto, observe a figura em vermelho à direita:
Note que temos o número dois ( 2 ) com o número três ( 3 ) sobrescrito à sua direita ( 23 ). Dizemos que o número 2 está elevado à terceira potência, ou ainda que 23 é a terceira potência de 2.
Nesta potência o número 2 é a sua base e ao número 3 damos o nome de expoente.
Esta potência representa a multiplicação de três fatores iguais a dois, então 23 é igual a 2 . 2 . 2 que é igual a 8.
Potências com expoente 2 ou 3 possuem uma outra forma particular de leitura. A potência 23 também pode ser lida como dois ao cubo, assim como a potência 32 pode ser lida como três ao quadrado.
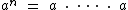 , isto é, a multiplicação de n fatores iguais a a.
, isto é, a multiplicação de n fatores iguais a a.
Este é o caso de mais fácil compreensão, pois o conceito da exponenciação está bem claro. Observe a expressão abaixo:

54, que se lê 5 elevado a 4, ou 5 elevado à quarta potência é igual ao produto de quatro fatores todos eles iguais a cinco. Ao multiplicarmos 5 vezes 5 vezes 5 vezes 5 iremos obter 625 que é o resultado da exponenciação. O número de fatores iguais a 5 é justamente o numeral do expoente.
Apesar de estarmos trabalhando com expoentes inteiros, as bases podem ser decimais:

Assim como também podem ser fracionárias:
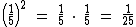


00 é indeterminado, embora em algumas situações convenciona-se que seja igual a 1. Para qualquer outro expoente real n positivo, temos que 0n = 0.
Mais à frente teremos outras informações que nos levarão a concluir que 00 = 0/0 e como não existe divisão por zero no conjunto dos números reais, trata-se então de uma indeterminação.
Ao estudarmos os expoentes negativos, a seguir, poderemos concluir que 0n é indefinido para qualquer n real negativo, por exemplo, 0-2 pode ser expresso como 1/02, o que nos leva à 1/0 e como sabemos, a divisão real de 1 por 0 é indefinida, pois não existe nenhum número real que multiplicado por 0 resulte em 1.
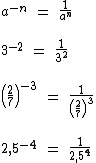
Vejamos agora a explicação onde se baseiam estes três últimos conceitos explicados acima.

Primeiramente vamos substituir as potências por suas respectivas multiplicações:

Repare que a expressão foi substituída pela multiplicação de 7 fatores iguais a a.
Pelo conceito da exponenciação podemos então escrever a seguinte potência:

De onde concluímos que:

Generalizando:

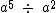
Substituindo as potências por suas respectivas multiplicações:

Utilizamos uma fração ao invés do operador ,
apenas para visualisarmos mais facilmente o próximo passo, que será a
simplificação de dois fatores do numerador com dois fatores do
denominador:
,
apenas para visualisarmos mais facilmente o próximo passo, que será a
simplificação de dois fatores do numerador com dois fatores do
denominador:

Do estudado até agora sabemos que:

Então chegamos a conclusão de que:
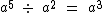
Novamente generalizando temos:

Note que a base a deve ser diferente de 0, pois como sabemos não existe quociente real para a divisão por zero neste conjunto numérico.

Então se tivermos m = n temos que:

Sabemos que:
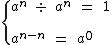
Já todo número, diferente de zero, dividido por ele mesmo é igual a 1 e que todo número menos ele mesmo é igual a zero.
Logo concluímos que:
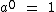
É por isto que todo número, diferente de zero, elevado a 0 é igual a 1:

Logo se tivermos m = n + 1 temos que:

Como:

Então:
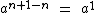
Logo:

Agora vamos transformar as potências do primeiro membro em multiplicações do fator a:
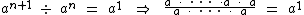
Repare que o numerador da fração no primeiro membro possui um fator a a mais que o denominador, pois o expoente da potência do numerador tem uma unidade a mais que o expoente da potência do denominador. Simplificando a fração temos:

Ou ainda:

Uma outra forma de entendermos porque a1 = a é que pela própria definição de potência, o expoente indica o número de fatores e como o expoente é igual a 1, obviamente este fator será o próprio número.

Se tivermos m = 0:

Como a0 = 1, temos:

Ou:
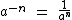

Vamos tomar como exemplo o produto de três fatores distintos elevados ao cubo:
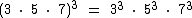
Não custa nada fazermos uma verificação só para conferir:


Exemplo:

Vamos verificar:


Exemplo:
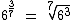
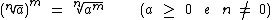
Exemplo:


Vamos como de costume recorrer a um exemplo:

E agora vamos verificar a veracidade desta propriedade:


Qual é a razão desta desigualdade?
No caso de devemos calcular
devemos calcular 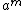 primeiro por causa da precedência dos parênteses, o que está entre parênteses deve ser calculado primeiro. Já no caso de
primeiro por causa da precedência dos parênteses, o que está entre parênteses deve ser calculado primeiro. Já no caso de  devemos calcular
devemos calcular 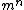 primeiro, pois neste caso a precedência é calcularmos do expoente mais externo para o mais interno.
primeiro, pois neste caso a precedência é calcularmos do expoente mais externo para o mais interno.
Usemos como exemplo a expressão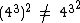 para verificarmos a desigualdade:
para verificarmos a desigualdade:
No primeiro membro iremos resolver primeiro 43 que é igual a 64, já no segundo membro vamos resolver primeiro 32 que é igual a 9:
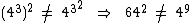
Finalmente vamos elevar 64 ao quadrado e 4 à nona potência:

Alternativamente também podemos realizar as seguintes operações, multiplicando os expoentes da potência do primeiro membro:


Note que temos o número dois ( 2 ) com o número três ( 3 ) sobrescrito à sua direita ( 23 ). Dizemos que o número 2 está elevado à terceira potência, ou ainda que 23 é a terceira potência de 2.
Nesta potência o número 2 é a sua base e ao número 3 damos o nome de expoente.
Esta potência representa a multiplicação de três fatores iguais a dois, então 23 é igual a 2 . 2 . 2 que é igual a 8.
Potências com expoente 2 ou 3 possuem uma outra forma particular de leitura. A potência 23 também pode ser lida como dois ao cubo, assim como a potência 32 pode ser lida como três ao quadrado.
Potências de Base Real com Expoente Inteiro
Nestas condições há quatro situações em particular que
iremos tratar. A saber, quando o expoente é maior que um, quando é igual
a um, quando é igual a zero e quando é negativo.
Expoente Maior que 1
De forma geral:
Este é o caso de mais fácil compreensão, pois o conceito da exponenciação está bem claro. Observe a expressão abaixo:
54, que se lê 5 elevado a 4, ou 5 elevado à quarta potência é igual ao produto de quatro fatores todos eles iguais a cinco. Ao multiplicarmos 5 vezes 5 vezes 5 vezes 5 iremos obter 625 que é o resultado da exponenciação. O número de fatores iguais a 5 é justamente o numeral do expoente.
Apesar de estarmos trabalhando com expoentes inteiros, as bases podem ser decimais:
Assim como também podem ser fracionárias:
Expoente Igual a 1
Todo número elevado a 1 é igual ao próprio número:
Expoente Igual a 0
Todo número, diferente de zero, elevado a 0 é igual a 1:
00 é indeterminado, embora em algumas situações convenciona-se que seja igual a 1. Para qualquer outro expoente real n positivo, temos que 0n = 0.
Mais à frente teremos outras informações que nos levarão a concluir que 00 = 0/0 e como não existe divisão por zero no conjunto dos números reais, trata-se então de uma indeterminação.
Ao estudarmos os expoentes negativos, a seguir, poderemos concluir que 0n é indefinido para qualquer n real negativo, por exemplo, 0-2 pode ser expresso como 1/02, o que nos leva à 1/0 e como sabemos, a divisão real de 1 por 0 é indefinida, pois não existe nenhum número real que multiplicado por 0 resulte em 1.
Expoente Negativo
Qualquer número diferente de zero elevado a um expoente negativo é igual ao inverso deste número elevado ao oposto do expoente:
Vejamos agora a explicação onde se baseiam estes três últimos conceitos explicados acima.
Propriedades das Potências de Base Real com Expoente Inteiro
Multiplicação de Potências de Mesma Base
A multiplicação de potências de mesma base é igual a esta base elevada à soma dos expoentes.
Vamos analisar o desenvolvimento da expressão a elevado à quinta potência vezes a elevado ao quadrado para confirmarmos esta afirmação:Primeiramente vamos substituir as potências por suas respectivas multiplicações:
Repare que a expressão foi substituída pela multiplicação de 7 fatores iguais a a.
Pelo conceito da exponenciação podemos então escrever a seguinte potência:
De onde concluímos que:
Generalizando:
Divisão de Potências de Mesma Base
A divisão de potências de mesma base, diferente de zero, é igual a esta base elevada à diferença dos expoentes.
Vamos utilizar as mesmas potências analisadas na propriedade anterior, mas agora fazendo a análise em relação à divisão:Substituindo as potências por suas respectivas multiplicações:
Utilizamos uma fração ao invés do operador
Do estudado até agora sabemos que:
Então chegamos a conclusão de que:
Novamente generalizando temos:
Note que a base a deve ser diferente de 0, pois como sabemos não existe quociente real para a divisão por zero neste conjunto numérico.
Entendendo porque a0 = 1
Para a ≠ 0 sabemos que:Então se tivermos m = n temos que:
Sabemos que:
Já todo número, diferente de zero, dividido por ele mesmo é igual a 1 e que todo número menos ele mesmo é igual a zero.
Logo concluímos que:
É por isto que todo número, diferente de zero, elevado a 0 é igual a 1:
Entendendo porque a1 = a
Para a ≠ 0 sabemos que:Logo se tivermos m = n + 1 temos que:
Como:
Então:
Logo:
Agora vamos transformar as potências do primeiro membro em multiplicações do fator a:
Repare que o numerador da fração no primeiro membro possui um fator a a mais que o denominador, pois o expoente da potência do numerador tem uma unidade a mais que o expoente da potência do denominador. Simplificando a fração temos:
Ou ainda:
Uma outra forma de entendermos porque a1 = a é que pela própria definição de potência, o expoente indica o número de fatores e como o expoente é igual a 1, obviamente este fator será o próprio número.
Entendendo porque a-n = 1/an
Como já vimos para a ≠ 0 temos que:Se tivermos m = 0:
Como a0 = 1, temos:
Ou:
Potência de um Produto
A potência do produto de dois ou mais fatores é igual ao produto de cada um destes fatores elevados ao expoente em questão:
Vamos tomar como exemplo o produto de três fatores distintos elevados ao cubo:
Não custa nada fazermos uma verificação só para conferir:
Potência de um Quociente
Podemos proceder de forma análoga ao que fizemos no caso
da multiplicação, mas neste caso os divisores não podem ser iguais a
zero:
Exemplo:
Vamos verificar:
Potência de um Expoente Fracionário
Podemos transformar uma potência com expoente fracionário em um radical:
Exemplo:
Potência de uma Raiz
Ao elevarmos um radical
a uma dada potência, estaremos obtendo o mesmo resultado que obteríamos
se elevássemos apenas o seu radicando a esta mesma potência:
Exemplo:
Potência de uma Potência
Novamente para uma base diferente de zero podemos expressar a seguinte igualdade:
Vamos como de costume recorrer a um exemplo:
E agora vamos verificar a veracidade desta propriedade:
Você sabe por que 2 + 3 . 5 é igual a 17 e não igual a 25?
Simplesmente porque o operador da multiplicação tem precedência sobre o operador da adição. Você deve primeiro realizar a multiplicação e depois a adição. Agora veja a expressão abaixo:Qual é a razão desta desigualdade?
No caso de
Usemos como exemplo a expressão
No primeiro membro iremos resolver primeiro 43 que é igual a 64, já no segundo membro vamos resolver primeiro 32 que é igual a 9:
Finalmente vamos elevar 64 ao quadrado e 4 à nona potência:
Alternativamente também podemos realizar as seguintes operações, multiplicando os expoentes da potência do primeiro membro:
Assinar:
Comentários (Atom)