RACHMANINOFF RHAPSODY tema do filme "Somewhere in the Time" Em algum lug...

 "Talvez algum dia a gente se reencontre,talvez não,a distância que nos separa pode ser física,mas não espiritual,sei que em algum momento a gente vai relembrar de tantas coisas que poderiam ser ditas e feitas,mas que talvez não deu tempo,mas o que fortalece é saber que tudo que é bom dura pouco,mas dura o suficiente para se tornar inesquecível,hoje mais uma vez desabei,as lembranças acabam comigo e junto com ela a saudade me mata,sempre pergunto o por quê?Tem coisas que simplesmente temos que procurar ser fortes e seguir,mas certamente hoje não estou tão forte,sei que em algum lugar do passado muitas coisas ficaram e eu mais uma vez estou aqui com este sentimento que me perturba a alma..."                                          Rogério Dias.

Ariel Dias

NÚMEROS NATURAIS

Conjunto dos Números Naturais

Representação dos números naturais

Conjunto é a reunião de elementos que têm características em comum. Por exemplo: se pegarmos a reunião dos alunos do 6° ano de um colégio, irá pertencer a esse conjunto somente os alunos do 6° ano, qualquer outro aluno de qualquer outra turma não pertencerá a esse conjunto.

Dentro da matemática estudamos o conjunto dos números chamados de Conjuntos numéricos. Esses conjuntos são formados sempre por números.
Os conjuntos numéricos são:


Conjunto dos Naturais
Conjunto dos Inteiros
Conjunto dos Racionais
Conjunto dos Irracionais
Conjunto dos Reais

Para simplificar a escrita desses conjuntos cada um recebe um tipo de representação:
O conjunto dos Naturais é representado pela letra N (maiúscula), o conjunto dos Inteiros é representado pela letra Z (maiúscula), o conjunto dos Racionais é representado pela letra Q (maiúscula), o conjunto dos Irracionais é representado pela letra I (maiúscula) e o conjunto dos Reais é representado pela letra R (maiúscula).

Cada conjunto tem uma característica própria.

?Conjunto dos Naturais

Os números que pertencem ao Conjunto dos Naturais são os não decimais maiores e iguais a zero.

N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12...}

Dentro de um conjunto podemos tirar um subconjunto (conjunto retirado de dentro de outro conjunto), dentro do conjunto dos naturais temos o conjunto dos naturais menos o zero, esse conjunto é representado por N*:

N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12...}

• Quando vamos fazer a comparação de elemento com conjunto ou vice-versa utilizamos o símbolo de (pertence) e (não pertence):

Por Exemplo:
5  N

3,58 N

- 6  N

Representação Geométrica de N



A reta numérica dos naturais cresce apenas para a direita.
Por Alunos Online

CENTENÁRIO DA ASSEMBLEIA DE DEUS EM ALAGOAS

CENTENÁRIO DAS ASSEMBLEIAS DE DEUS NO ESTADO DE ALAGOAS

UMADDEL 2016

ESTE VÍDEO É LEGAL!

Números decimais,considero este vídeo um dos mais práticos para auxiliar as nossas aulas,bons estudos!

OPERAÇÕES COM NÚMEROS DECIMAIS

MATEMÁTICA

Realizar as operações de soma, subtração, multiplicação e divisão com números decimais requer o conhecimento de algumas regras que caracterizam esse conjunto.

Quando começamos a trabalhar com os números racionais, deparamo-nos com os números decimais, aqueles que possuem vírgula. Esses números possuem algumas características que merecem nossa atenção. Eles são formados por uma parte inteira e outra parte decimal, sendo que os números que estão do lado esquerdo da vírgula compõem a parte inteira, e os que estão à direita representam a parte decimal. Vejamos um exemplo:

                                      1,357
                                       |     |
Parte inteira  <------------------|       |------------------>     Parte Decimal

Quando desejamos realizar operações de adição ou de subtração, podemos utilizar o algoritmo de cada operação. Mas devemos nos lembrar de que a parte inteira deve somar apenas com outra parte inteira, do mesmo modo a parcela decimal deve ser operada com a outra que também é decimal. Para evitar enganos, é recomendável que façamos o algoritmo colocando sempre a vírgula embaixo de outra vírgula. Vejamos alguns exemplos:

Na imagem, temos alguns “zeros” em vermelho. Isso aconteceu porque nem sempre todos os números terão a mesma casa de números decimais e, a fim de melhorar nossos cálculos, devemos preencher com zeros os espaços vazios à direita.

Em se tratando de multiplicação, não há a necessidade de colocarmos vírgula embaixo de vírgula. Devemos realizar a multiplicação da forma tradicional, mas devemos lembrar que é necessário unir a quantidade de casas decimais. Por exemplo, o caso da multiplicação de 0,075 por 0,001. Ao fazermos a multiplicação normalmente, desconsiderando a vírgula, obtemos o resultado 75, mas o primeiro número tem três algarismos após a vírgula, e o segundo, três algarismos. Portanto, a resposta é 0,000075. Vejamos alguns exemplos:

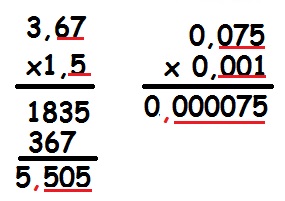
A divisão de números inteiros requer a nossa atenção para alguns detalhes. Vejamos os possíveis casos de divisões:

1º – Divisão de números inteiros

a) Quando o dividendo é maior que o divisor:

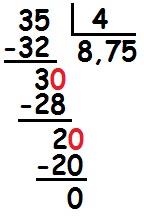
Nesse caso, poderíamos ter finalizado a divisão tendo como quociente o número 8 e deixando 3 como resto. Como demos continuidade, foi necessário acrescentar o zero ao fim dos números que seriam divididos para concluir a divisão. Quando é necessário fazer o acréscimo do zero, colocamos uma vírgula no quociente.

b) Quando o dividendo é menor que o divisor:

Nesse exemplo, queremos dividir 4 por 8. Mas para conseguir fazer esse cálculo, é necessário aumentar o dividendo. Então antes de iniciar a divisão, precisamos acrescentar um zero após o 4, transformando-o em 40. Ao fazer isso, colocamos um zero e uma vírgula no início do quociente para em seguida iniciar de fato a divisão. Caso fosse necessário, poderíamos colocar outro zero no dividendo, então haveria 400, e, no quociente, acrescentar outro zero após a vírgula, ficando com 0,0. É possível realizar esse processo quantas vezes forem necessárias.

2º – Divisão entre inteiros e decimais

a) Dividendo inteiro e divisor decimal

Quando precisamos dividir um número inteiro por outro que é decimal, é necessário tornar o dividendo também um número decimal. Para isso, basta acrescentar uma vírgula e um zero e verificar se o dividendo e o divisor possuem a mesma quantidade de números após a vírgula. Se for necessário, podemos acrescentar zeros até ficarem iguais. Feito isso, desconsideramos a vírgula e realizamos a divisão normalmente.

a) Dividendo decimal e divisor inteiro

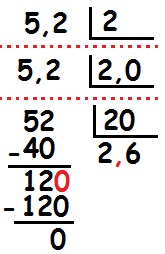
Semelhantemente ao caso anterior, precisamos que o divisor seja também um número decimal. Para tanto, acrescentamos nele a vírgula e um zero e verificamos se a quantidade de zeros após a vírgula é mesma para o divisor e para o dividendo. Feito isso, podemos realizar a divisão como de costume.

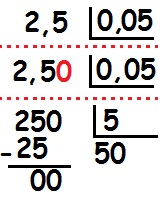
3º – Divisão entre decimais

Para realizar a divisão entre números decimais, é necessário que ambos tenham a mesma quantidade de números após a vírgula. Como já foi dito, acrescentamos zeros ao fim do número até que consigamos igualar a quantidade de casas decimais. Feito isso, desconsideramos as vírgulas e realizamos a divisão.

Por Amanda Gonçalves
Graduada em Matemática

AMIGO...

Significado de Amigo

Compartilhar

O que é Amigo:

Amigo é o nome que se dá a um indivíduo que mantém um relacionamento de afeto, consideração e respeito por outra pessoa. O amigo é aquele que possui uma grande afeição por uma ou mais pessoas, que é leal, que protege e faz o possível para ajudar sempre.
Para denominar uma pessoa de amigo, não necessariamente os indivíduos precisam se conhecer há muito tempo, muitas amizades começam repentinamente e ganham importância por diversos motivos. Amigo é aquela pessoa que se confia acima de qualquer coisa, que está sempre disposto a ajudar, seja em situações boas ou ruins.
Para chamar alguém de amigo, não necessariamente precisa ser apenas amigo. Existem muitos familiares, como primos, tios, namorados e até mesmo os próprios pais do indivíduo podem ser considerados um amigo, por sua postura e jeito de agir, por ser alguém sempre disposto a conversar e ajudar.
Em alguns momentos, o amigo não precisa ter necessariamente os mesmos gostos e vontades, e em certos casos é esse exatamente o fato que os une. O amigo não precisa ser alguém completamente idêntico. É aquele que tem o poder de acrescentar ao outro, com suas ideias, momentos de vida, informações etc., ou apenas alguém para dividir momentos e sentimentos.

Dia do Amigo

O amigo é tão importante na vida das pessoas, que criaram um dia próprio para ele. O dia do amigo é comemorado em 20 de julho. A data foi criada por um argentino, a partir da chegada do homem à lua, em 20 de julho de 1969. O argentinou resolveu enviar cartas para diversos países para instituir o Dia do Amigo, pois acreditava que a chegada à lua era um significado de que os homens deveriam se unir.

Melhor Amigo

Algumas pessoas intitulam seu amigo de “melhor amigo”, e muitas vezes esses se conhecem mais que algum membro da própria família. O melhor amigo consegue ser alguém melhor ainda que um amigo, o nível de lealdade, amizade, atenção, carinho e afeto é muito maior, e estes costumam estar sempre juntos, sendo confidentes e cúmplices.
A nomenclatura de melhor amigo é mais utilizada por mulheres, mas ambos os sexos tem seus próprios melhores amigos, que são aqueles que o indivíduo leva para toda vida, e está presente em todos os momentos.

Amigo Colorido

Existe também o amigo colorido,  que é o relacionamento que acontece entre homens e mulheres, e também pessoas do mesmo sexo. O amigo colorido é aquele onde mantém-se um envolvimento maior que amizade e afeto, é um relacionamento amoroso e sexual, onde os envolvidos continuam amigos, mas têm um contato maior, mais íntimo e intenso.
Em muitos casos o amigo colorido pode evoluir para um relacionamento amoroso, e virar namorado, noivo e até mesmo marido.

Relatos de amigos

Nas artes existem diversos relatos e demonstrações de amizades, sejam elas através de poemas, filmes, literatura e canções. O cantor Roberto Carlos, por exemplo, compôs uma canção chamada “Amigo” que tornou-se muito famosa, e é conhecida até os dias atuais. Existem também diversos poemas falando sobre amigos, como o poema grego chamado de “Poema de Gilgamesh”.
A própria Bíblia cita a amizade, falando em 1 Samuel (capítulo 18) sobre a forte amizade entre Jônatas e Davi. Algumas obras, como Dom Quixote e Sancho Pança, Sherlock Holmes e Os Três Mosqueteiros, relatam a relação com um ou mais amigos. Existem também filmes e séries de televisão, como O gordo e o magro, Os três patetas, Friends, entre muitos outros.

ANIVERSÁRIO DA MINHA QUERIDA MÃE,MACEIÓ,04 DE FEVEREIRO DE 2017,SÁBADO

PARABÉNS MINHA QUERIDA MÃE...

Agradeço a Deus pela tua existência,sei que os dias estão sendo difíceis,mas creio no milagre sobrenatural de Deus na tua vida mainha,só peço a ele que conceda muitos anos de vida para que possamos nos alegrar por muitos dias ao teu lado,parabéns!