ROGÉRIO DIAS

domingo, 13 de agosto de 2017

VALENTINA VEM AÍ...

Está chegando o momento dela vir ao mundo e certamente é muito esperada,ontem aconteceu o chá de bebê de Valentina,um momento realmente muito bom,que venha com muita saúde,pois amor é o que não vai faltar,parabenizamos os pais:William e Morgana...

terça-feira, 11 de julho de 2017

SISTEMA DE EQUAÇÃO

Sistema linear

Por Marcos Noé

Os sistemas de equações consistem em ferramentas importantes na Matemática, eles são utilizados para determinar os valores de x e y nas equações com duas variáveis. A resolução dos sistemas consiste em estabelecer uma relação entre as equações e aplicar técnicas de resolução. Os métodos usados na resolução de um sistema são: substituição e adição. Exemplos de sistemas de equações:

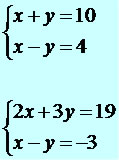
Método da Substituição

O método da substituição consiste em trabalhar qualquer equação do sistema de forma a isolar uma das incógnitas, substituindo o valor isolado na outra equação. Observe passo a passo a resolução do sistema a seguir:

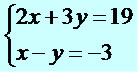
Nesse caso, vamos escolher a 2º equação e isolar a incógnita x.

x – y = –3
x = –3 + y

Agora, substituímos o valor de x por –3 + y na 1º equação.

2x + 3y = 19
2*(–3 + y) + 3y = 19
–6 + 2y + 3y = 19
2y + 3y = 19 + 6
5y = 25
y = 5

Para finalizar, calculamos o valor de x utilizando a seguinte equação:

x = –3 + y
x = –3 + 5
x = 2

Portanto, a solução do sistema é x = 2 e y = 5, isto é, o par ordenado (2,5)

Método da Adição

O método da adição deve ser utilizado nos sistemas em que existe a oportunidade de zerar uma das incógnitas. Observe a resolução do sistema a seguir:

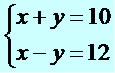
1º passo: somamos as equações, eliminando uma das incógnitas e determinando o valor da outra incógnita.

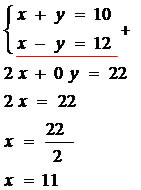
Calculado o valor de x, basta escolher uma das equações e substituir o valor de x por 11.

x + y = 10
y = 10 – x
y = 10 – 11
y = –1

A solução do sistema é o par ordenado (11, –1).

Por Marcos Noé

segunda-feira, 3 de julho de 2017

MODELO DE TCC

Sempre o famoso tcc,ou seja,o trabalho de conclusão de curso traz uma grande dor de cabeça para os alunos que estão concluindo a sua formação,vamos dar uma valiosa dica de modelo estrutural:

Estrutura Básica De Um TCC

Pré
Textuais

·
Capa

·
Folha de rosto

·
Folha de aprovação

·
Dedicatória

·
Agradecimentos

·
Epígrafe

·
Resumo

·
Sumário

·
Lista de ilustrações

·
Listas de abreviaturas e siglas

·
Listas de notações

Textuais

·
Introdução

·
Desenvolvimento

·
Estudo de Caso

·
Conclusão ou Considerações finais

Pós Textuais

·
Bibliografias (referências) – Muito importantes

Vale salientar que com esta grande dica que vou lhe passar, você poupará muito tempo que poderá usar para fazer outras coisas, pois assim terminará seu trabalho rapidamente e sem perder a qualidade.